Table Of Content

In dummy coding, a binary variable, a reference group (e.g., a control group) is assigned a value of zero (0) and the other group (e.g., an active treatment group) is assigned a value of one (1). Effect coding of a binary variable is the same except that the zero for the reference group is replaced with −1. A research design should reflect the goals of the research endeavor. In general, if the major goal of a study is to contrast directly one “treatment” with another treatment (e.g., a control treatment), then an RCT is usually the best choice. Note that here “treatment” is used to connote a set of intervention components (ICs); e.g., a particular type, dose, and duration of medication, type of counseling that is delivered for a particular number of sessions of a particular duration, and so on.
3.1. 2x2 Factorial designs¶
One Factor at a Time and factorial experimental design for formulation of l-carnitine microcapsules to improve its ... - ScienceDirect.com
One Factor at a Time and factorial experimental design for formulation of l-carnitine microcapsules to improve its ....
Posted: Mon, 15 Jan 2024 08:00:00 GMT [source]
However the other two combinations, A and C and A and D, indicate that significant interaction exists. If you just looked at the main effects plot you would likely miss the interactions that are obvious here. The analysis of variance summary table results show us that the main effects overall are significant.
Main Effects
These can be very helpful to understand and present the relationship between several factors on the response. The contour plots below for our example show the color coded average response over the region of interest. The effect of these changes in colors is to show the twist in the plane. And you picked your low and high level as illustrated above, then you would have missed capturing the true relationship. Your conclusion would probably be that there is no effect of that factor.
ThinkBook Plus Reinvents Rotating Display Form Factor with New Twist Design - Lenovo StoryHub
ThinkBook Plus Reinvents Rotating Display Form Factor with New Twist Design.
Posted: Thu, 05 Jan 2023 08:00:00 GMT [source]
3 - Unreplicated \(2^k\) Factorial Designs
It’s the difference between performance in the Distraction and No-Distraction conditions. In general, it is very common to use the word effect to refer to the differences caused by the IV. We manipulated distraction, it caused a difference, so we call this the “distraction effect”. The quantities b1, b2, and so on are regression weights that indicate how large a contribution an independent variable makes, on average, to the dependent variable. Specifically, they indicate how much the dependent variable changes for each one-unit change in the independent variable.
Other designs such as Plackett-Burman or a General full factorial design can be chosen. For information about these designs, please refer to the "Help" menu. The following Yates algorithm table using the data for the null outcome was constructed. As seen in the table, the values of the main total factorial effect are 0 for A, B, and AB. This proves that neither dosage or age have any effect on percentage of seizures. A design which manipulates one independent variable between subjects and another within subjects.
Traditionally, experiments are designed to determine the effect of ONE variable upon ONE response. Fisher showed that there are advantages by combining the study of multiple variables in the same factorial experiment. Factorial design can reduce the number of experiments one has to perform by studying multiple factors simultaneously. Additionally, it can be used to find both main effects (from each independent factor) and interaction effects (when both factors must be used to explain the outcome). However, factorial design can only give relative values, and to achieve actual numerical values the math becomes difficult, as regressions (which require minimizing a sum of values) need to be performed. Regardless, factorial design is a useful method to design experiments in both laboratory and industrial settings.
Assigning Participants to Conditions
Higher order interactions can reflect complex patterns that defy easy interpretation. However, they also reveal information that is unique and of potentially great value. Further, this problem is reduced if factorial designs are used as screening experiments, whose purpose is not to identify the single best combination of ICs (Collins et al., 2009). Rather such experiments are used to identify the ICs that are amongst the best. Therefore, finding that several combinations of ICs yield promising effects is compatible with the goal of a screening experiment, which is to distill the number of ICS to those holding relatively great promise. In keeping with this, the data in Figure 1 suggest that we can winnow potentially promising combinations from 16, to 3.
How is this related to Factorial Designs?
Manipulation checks become especially important when the manipulation of the independent variable turns out to have no effect on the dependent variable. Imagine, for example, that you exposed participants to happy or sad movie music—intending to put them in happy or sad moods—but you found that this had no effect on the number of happy or sad childhood events they recalled. This could be because being in a happy or sad mood has no effect on memories for childhood events. But it could also be that the music was ineffective at putting participants in happy or sad moods.
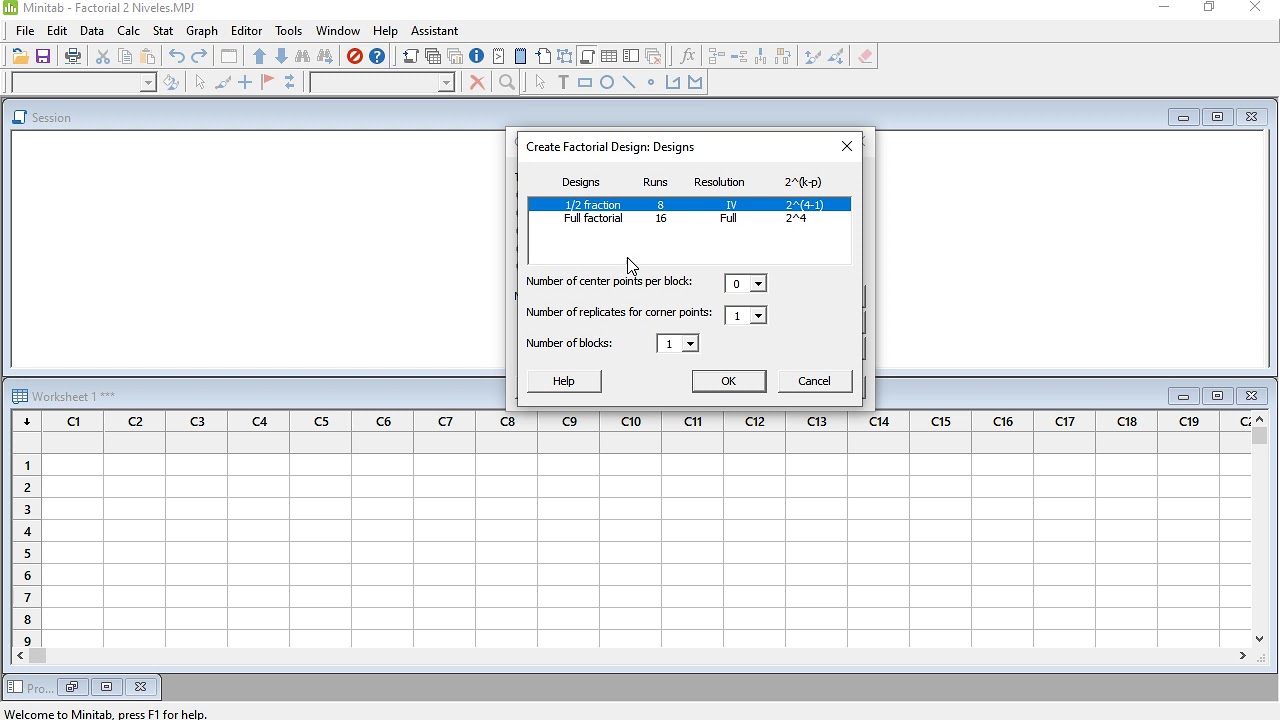
Creating a Factorial Design in Minitab
In many cases, though, the factor levels are simply categories, and the coding of levels is somewhat arbitrary. For example, the levels of an 6-level factor might simply be denoted 1, 2, ..., 6. Regardless of whether the design is between subjects, within subjects, or mixed, the actual assignment of participants to conditions or orders of conditions is typically done randomly. We will set this up the same way in Minitab and this time Minitab will show the plot in three dimensions, two variables at a time.
A contrast in cell means is a linear combination of cell means in which the coefficients sum to 0. Contrasts are of interest in themselves, and are the building blocks by which main effects and interactions are defined. Treatment combinations are denoted by ordered pairs or, more generally, ordered tuples. In the aquaculture experiment, the ordered triple (25, 80, 10) represents the treatment combination having the lowest level of each factor. In a general 2×3 experiment the ordered pair (2, 1) would indicate the cell in which factor A is at level 2 and factor B at level 1.
There is one possible main effect for each independent variable in the design. When we find that independent variable did influence the dependent variable, then we say there was a main effect. When we find that the independent variable did not influence the dependent variable, then we say there was no main effect. When researchers combine dependent variables in this way, they are treating them collectively as a multiple-response measure of a single construct.
If more than one outcome variable is used in analyses, the number of models computed and effects tested grow quickly. Various approaches have been suggested for dealing with the challenge posed by so many statistical comparisons being afforded by complex factorial designs (Couper et al., 2005; Green, Liu, & O’Sullivan, 2002). As opposed to an RCT, where the focus is on demonstrating effects that are highly unlikely to be due to chance, the screening experiment is focused on relative promise of the tested ICs. Factorial design is an important method to determine the effects of multiple variables on a response.
Imagine, for example, that a researcher conducts an experiment on the effect of daily exercise on stress. The dependent variable, stress, is a construct that can be operationalized in different ways. For this reason, the researcher might have participants complete the paper-and-pencil Perceived Stress Scale and also measure their levels of the stress hormone cortisol. If the researcher finds that the different measures are affected by exercise in the same way, then he or she can be confident in the conclusion that exercise affects the more general construct of stress. When an experiment includes multiple dependent variables, there is again a possibility of carryover effects.
Did manipulation of the independent variables cause changes in the dependent variables? However, 2x2 designs have more than one manipulation, so there is more than one way that the dependent variable can change. Often a researcher wants to know how an independent variable affects several distinct dependent variables.
If an investigator decides to use a factorial design, s/he has numerous choices to make, including choices about the number and types of factors to include. As an exercise toward this goal, we will first take a closer look at extracting main effects and interactions from tables. This exercise will how the condition means are used to calculate the main effects and interactions. This framework can be generalized to, e.g., designing three replicates for three level factors, etc.

No comments:
Post a Comment